 |
|
| |
|
Frequenzweichen
Einleitung: Da ich nicht die gesamte Erklärung
sämtlicher Grundlagen übernehmen kann, versuche ich hier
nur einige praktische Erklärungen an der Oberfläche zu
geben. Wer sich hierfür genau interessiert, sollte sich
bei entsprechender Vorbildung wohl oder übel mit einem
Fachbuch auseinander setzen. Zumal man für das Erstellen
der Leiterplatte nachher ja eh Kenntnisse und etwas
Erfahrung besitzen sollte. Über Grundlagen in Elektronik
und einfache Mathematik sollte man dennoch verfügen...
Da die Zeit für mich zum Beantworten von mails eng ist,
bitte ich auf genaue Anfragen zur Berechnung einzelner
Weichen zu verzichten.
Da auch ich mich mal bei einigen Dingen mal verrechnen oder irren kann, gebe ich keine Garantie für sämtliche Inhalte auf dieser Seite (wie alle anderen einzelnen Seiten bei www.selfmadehifi.de auch )
Ich gehe hier nur auf analoge Filter ein, digitale arbeiten gänzlich anders.
Die Aufgabe von Frequenzweichen in der Akustik ist es, den gesamten hörbaren Bereich in einzelne Bereiche zu unterteilen.
Typen: Man benutzt hauptsächlich Tief-, Band- und
Hochpässe in der Akustik. Ein Tiefpass (Integrierglied)
lässt verstärkt tiefe Frequenzen durch und dämpft hohe,
bei einem Hochpass (Differenzierglied) ist es umgekehrt.
Ein Bandpass lässt mittlere Frequenzen (ein Frequenzband)
durch und dämpft Frequenzen darunter und darüber. Er
entsteht oft durch einfaches (aber entkoppeltes!)
Nacheinanderschalten eines Hoch- und eines Tiefpasses.
Bandsperren dämpfen ein Frequenzband, lassen den
restlichen Bereich aber hindurch. Das lässt sich mit einem
Kerbfilter (auch Notch-Filter genannt) weiter steigern,
der nur eine Frequenz aus einem Bereich extrem stark
dämpft. Allpässe sind eher selten, sie weisen eine
Phasenverschiebung abhängig von der Frequenz auf, der
Amplitudenverlauf bleibt dabei konstant.
Noch etwas:
Ein Frequenzweichen-Zweig wird (neben dem Typ) durch die
Grenzfrequenz, Flankensteilheit und Güte charakterisiert.
Die Grenzfrequenz fg (oder englisch fc cut frequency) gibt
die Frequenz des Filters an, bei der die Spannung auf ca.
70,7% abgefallen ist, das sind etwa 3 dB und ist der Punkt
der Leistungshalbierung.
Die Flankensteilheit zeigt, wie stark das Filter im zu dämpfenden Frequenzbereich wirkt. Bei Hoch- und Tiefpässen 1. Ordnung (nur ein passives Bauteil für den Filter) beträgt sie 6 dB/Oktave, was 20 dB/Dekade entspricht. Das bedeutet z.B. bei einem Tiefpass über der Grenzfrequenz mit jeder Verzehnfachung der Frequenz der Pegel um 20 dB abnimmt, was nun mal 6 dB bei der Frequenzverdoppelung sind. Hochpass- und Tiefpass-Filter 2. Ordnung dämpfen mit 12 dB/Oktave, 3. Ordnung mit 18 dB u.s.w. Passive Filter arbeiten meist von 1. bis maximal 4. Ordnung. Darüber werden üblicherweise nur noch aktive Filter benutzt, die durch Nacheinanderschalten extrem steile Flanken erlauben.
Bei Bandpässen ist die Definitionen anders: Der E-Techniker spricht von Bandpässen 2. Ordnung, obwohl sie nach oben und unten nur mit 6 dB/Okt. dämpfen. Grund: Gemeint ist die mathematische Ordnung: der Grad des Polynoms im Nenner der Übertragungsfunktion G(f). Das heißt, Bandpässe, die zu hohen und tiefen Frequenzen mit der gleichen Flankensteilheit arbeiten (Standard), haben immer eine geradzahlige Ordnung.
Passive Weichen teilen den Frequenzbereich direkt
vor dem Lautsprecher. Passiv deshalb, weil sie keine
aktiven Bauelemente (Transistoren, Operationsverstärker)
enthalten. Eine passive Weiche besteht im allgemeinen nur
aus Kondensatoren (Kapazitäten C), Spulen (Induktivitäten
L) und ohmschen Widerständen (R). Im Prinzip stellen
komplexe Bauelemente (C, L) einen frequenzabhängigen
Widerstand dar. Bei Spulen erhöht er sich mit ansteigender
Frequenz, bei Kondensatoren sinkt er, bei Widerständen
bleibt er konstant. Durch entsprechende Anordnung können
diverse Filter mit unterschiedlichen Verhalten aufgebaut
werden.
Wie passive Frequenzzweige berechnet werden, kann man sich
äußerst einfach in BassCADe (ist
hier downloadbar) anschauen und simulieren lassen.
In der Praxis werden z.B. bei Lautsprechern meistens
Filter 2. Ordnung benutzt, Hoch- und Tiefpässe 1. oder 3.
Ordnung gibt es jedoch hierbei auch, sind aber seltener.
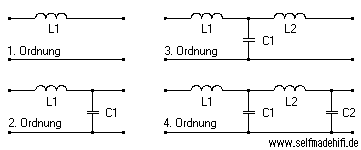
Das folgende Bild zeigt den Aufbau passiver Tiefpässe, bei
Hochpässen werden bei gleicher Anordnung nur die Spulen
(L) mit den Kondensatoren (C) ausgetauscht. Als Abschluss
dient jeweils ein Lautsprecher. Das ist quasi ein
Widerstand, der jedoch nicht frequenzneutral ist und
deshalb (leider) so die Charakteristik ebenfalls
beeinflusst.
Auf passive Weichen gehe ich hier nicht weiter ein, da die
oben genannte Software ausreichend Erklärungen,
Berechnungen und Simulationsmöglichkeiten einzelner
Weichenzweige bietet.
Bei Tiefpässen erster Ordnung gilt:
L=Z/(2*pi*fc)
bzw. bei RC-Tiefpässen äquivalent:
C=1/(2*pi*fc*R)
Bei Hochpässen:
C=1/ (2*pi*fc*Z)
äquivalent bei RC-Gliedern: C=1/(2*pi*fc*R)
Bei aktiven Weichen geschieht das alles vor der
Endstufe. Eine aktive Weiche arbeitet mit mindestens einem
aktiven BE (Bauelement), das die Abschwächung ausgleichen
soll. Die RC-Größenordnungen unterscheiden sich dabei, da
hier hoch- und mittelohmig gearbeitet wird. Grund dafür
sind geringere Ströme und kleinere Bauelemente (Rs und
Cs). Hierbei werden jedoch üblicherweise neben den aktiven
BE (im allgemeinen heute Operationsverstärker OP/OPV) nur
Kondensatoren und Widerstände benutzt. (Spulen sind im
NF-Bereich zu groß, verlustreich und unpraktisch.) Durch
entsprechende Anordnung der Bauteile z.B. in
Rückkopplungszweigen werden hier verschiedene
Frequenzverläufe erzeugt. Hierzu wird oft der OP in
invertierender Weise (wegen der einfachen
Verstärkungsberechnung V= Z2 / Z1) betrieben. Diese
Schaltungen hier gelten alle ohne Offset, das bedeutet
eine symmetrische Spannungsversorgung (plus minus x Volt
mit Mittelanzapfung 0 V an Masse) für den OP.
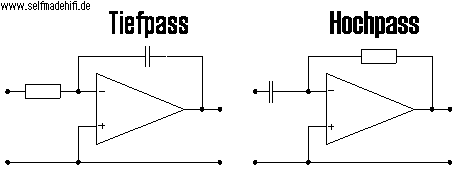
Hier sind die Grundprinzipien eines aktiven Tief- und
eines Hochpassfilters 1. Ordnung mit einem OP in
invertierender Bauweise. Das Ausgangssignal hat gegenüber
dem Eingangssignal eine Phasendrehung von 180°. Das heißt
hier invertiert, also eine positive Eingangsspannung
ergibt eine negative Aussgangspannung und umgekehrt.
Da jedes Filter ein gedämpftes schwingendes System darstellt, gibt die Güte die Unterdrückung dieser Schwingung bei der Resonanzfrequenz des Filters fr an. Je stärker das Schwingen unterdrückt wird, desto besser sind die Impuls- und Sprungantworten. Beim Hören zeigt sich das durch eine deutlich präzisere und impulsivere Wiedergabe. Standardfilter, die die meisten Quellen nach Formeln empfehlen, besitzen eine Güte von 0,707, so dass hier Resonanz- und Grenzfrequenz übereinstimmen. Sie sind deshalb auch einfacher zu berechnen, da die Werte gleich bleiben, wenn man die (entkoppelten) Bauelemente austauscht und aus einem Hoch- z.B. einen Tiefpass macht. In der Praxis wählt man besonders bei teuren Komponenten wegen der besseren Impulsivität etwas geringere Güten zwischen 0,5 und 0,6.
- Q<0,5 überdämpft (keine Schwingungsneigung)
- Q=0,5 (Linkwitz-Abstimmung, "Filter kritischer Dämpfung") Präzision hervorragend, Pegel bei der Einbauresonanz fc -6 dB, keinerlei Überschwingen in der Sprungantwort
- Bessel-Abstimmung: konstante Gruppenlaufzeit sehr gute Präzision, bei 2. Ordnung Q=0,577, Pegel bei fc ist -4,8 dB
- Q=0,707 (Butterworth-Abstimmung), noch gute Präzision, Pegel bei fc (ist hier immer untere Grenzfrequenz) -3 dB
- Q=1 (>0,707 Chebycheff-Abstimmung), schlechte Präzision, Pegel ist (Qtc=1) bei fc 0 dB, deshalb Überschwingen
Bessel-Filter (aka Thomson-Filter) besitzen ein hervorragendes Rechteckverhalten, da sie eine frequenzproportionale Phasenverschiebung aufweisen. Durch die starke Dämpfung schwingen sie bei der Sprungantwort extrem wenig und auch Filter höherer Ordnung klingen schnell ab.
Diese Filtertypen oder -Charakteristiken werden durch bestimmte Pol- und Nullstellenlage der Übertragungsfunktion gekennzeichnet.
Mit einer OP-Stufe lässt sich relativ leicht ein Filter 2. Ordnung aufbauen. Durch Umdimensionieren kann man das auch auf 3. Ordnung erweitern. (wie bei passiven Weichen)
Filter höhere Ordnung haben aber noch einen anderen Nachteil: Mit steigender Ordnung steigt die Gruppenlaufzeit.
Normalerweise ist das Errechnen von Filtern anhand der Koeffizenten aufwendig, weshalb ich den ganzen weiteren theoretischen Teil übersprungen habe, um alles zu vereinfachen. Es werden nur einige oft benutzte Möglichkeiten vorgegeben.
Dazu folgende Beispiele:
Eine relativ weit verbreitete Standard-Frequenzweiche 3.
Ordnung:
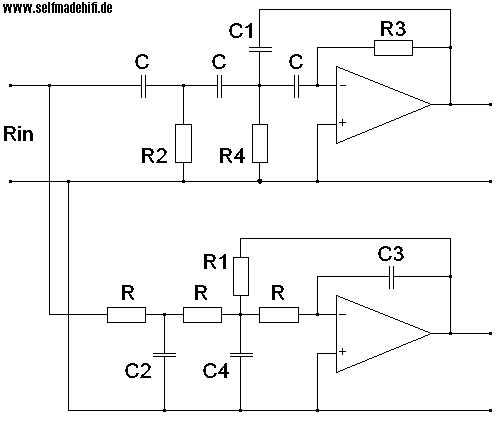
Die Werte für die Butterworth-Charakteristik:
Eingangswiderstand Rin (typ.Bereich 1 ... 20 kOhm)
R=Rin/2.
Im Allgemeinen nimmt man C doppelt so groß wie C2, wenn fu=fo, also C1=C2
| Tiefpass | Hochpass |
| C2=1/(2,5590*fo*R) | R2=1/(15,4226*fu*C) |
| C3=1/(32,5385*fo*R) | R3=1/(1,21377*fu*C) |
| C4=1/(2,9794*fo*R) | R4=1/(13,2501*fu*C) |
| R1=2*R | C1=C/2 |
| fo=1/(2*pi*R*cubrt(C2*C3*C4)) | fu=1/(2*pi*C*cubrt(R2*R3*R4)) |
Meist werden aber OPV-Stufen nur als Filter 2. Ordnung
aufgebaut, und diese dann nacheinander geschalten. Das hat
u.a. den Vorteil, dass man bei konstanter Güte nur durch
Widerstandsveränderung die Grenzfrequenz einfach verändern
kann. Das wird bei Subwooferweichen sehr gern gemacht. In
nicht invertierender Weise sieht das dann ungefähr so aus:
Tiefpass:
Bei diesen Filtern 2. Ordnung wählt man R1=R2 und C1=C2.
Die jeweilige Frequenz wird durch das RC-Glied (T=R*C)
bestimmt und beträgt etwa f=1/(6.3*RC)
Schaltet man 2 dieser Stufen hintereinander, erreicht man
einen Tiefpass 4. Ordnung mit 24dB/Oktave, der sich sehr
gut als Subwooferweiche (Mono) verwenden lässt. Durch die
komplette Rückkopplung ohne Widerstand ergibt sich eine
Gesamtverstärkung von 1.
Leider ist es durch die 4. Ordnung nötig 4 Widerstände zu
verändern, also sind 2 Tandem-Potis (bei mono!) mechanisch
zu koppeln oder besser ein Stufenschalter zu verwenden.
Für Besselcharakteristik gilt dann:
(Normalerweise legt man ja auch zuerst das C fest und
errechnet die Widerstände daraus... Aber ich mach' es hier
andersherum.)
R1=R2=R11=R12 (Summe aus Poti und Widerstand) in etwa der
Größe des Eingangswiderstands, also etwa 1 k ... 100 kOhm
Beim Einstellen gilt: je größer R, desto kleiner die
Frequenz, also mit den jeweiligen Festwiderstand und dem
zugehörigen Poti den Bereich (Verhältnis Rmax zu Rmin)
festlegen.
Aus den festgelegten Widerstandswerten (4 Festwiderstände
und 2 Tandempotis) die zugehörigen Kondensatoren
errechnen.
| 1. Stufe: | 2. Stufe: |
| C1=1/(8,47*fc*R) | C11=1/(6,16*fc*R) |
| C2=1/(9,24*fc*R) | C12=1/(15,8*fc*R) |
Da man aber ein Mono-Signal am Eingang braucht und nicht
nur einen Seitenkanal verwenden sollte, ist noch eine
Mischstufe vorzuschalten, also entweder je eine
Transistorstufe am besten in Emitterschaltung, oder
ebenfalls 2 OPVs, es geht auch mit nur einem OPV.
Der Aufbau des Hochpasses erfolgt in gleicher Weise, nur
werden in der Anordnung wieder alle Widerstände mit den
Kondensatoren vertauscht. Die Gleichungen gelten dann
(Güte würde sich sonst auf über 0,7 erhöhen) jedoch nicht
mehr.
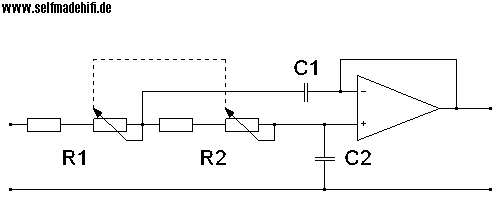
Hier ist als Beispiel ein aktiver Hochpass 2. Ordnung mit einer regelbaren Grenzfrequenz.
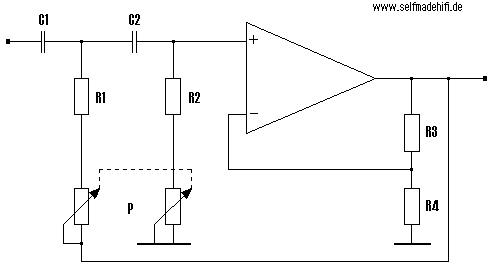
Für eine aktive Subwooferabkopplung wird eine regelbare
Trennfrequenz im Bereich zwischen 20...200 Hz benötigt.
Dafür ergeben sich dann folgende Werte (Butterworth)
C1=C2=150 nF; R1=R2= 4,7k; R3=R4= 10k; P: Tandempoti mit 2
mal 47 kOhm/lin.
Schaltet man n Tiefpässe gleicher Grenzfrequenz, Güte und Flankensteilheit hintereinander, gilt folgende Näherung:
| bei Tiefpässen (Anzahl n, Grenzfrequenz eines TP
fgi): fg=fgi/sqrt(n) |
bei Hochpässen (Anzahl n, Grenzfrequenz eines HP
fgi): fg=fgi*sqrt(n) |
weitere Links:
FilterPro Software von Texas Instruments: http://focus.ti.com/docs/toolsw/folders/print/filterpro.html
http://www.aktivfilter.de
Hier die Schaltung zu einer Phono-Vorstufe.